Iteration¶
This demonstrates the use of iteration both in the initialization phase, as well as execution, in order to reach convergence between federates.
Where is the code?¶
This example on Iteration. If you have issues navigating the examples, visit the HELICS Gitter page or the user forum on GitHub.
What is this co-simulation doing?¶
This example shows how to use set up the iteration calls that support state convergence across federates. This is discussed in more detail in the User Guide.
Differences Compared to the Advanced Default Example¶
This example changes the model of the default example so that the charger voltage is a function of the battery current: \(V_{ch}(I_{b})\). Conversely, battery current is a function of charger voltage: \(I_{b}(V_{ch})\). As a result, each time step requires some iteration to find the converged fixed-point, where both models are in a consistent state.
In very loose terms, the charging strategy uses constant current below a specific state of charge followed by constant voltage once rated voltage is achieved:
 source: https://batteryuniversity.com/article/bu-409-charging-lithium-ion
source: https://batteryuniversity.com/article/bu-409-charging-lithium-ion
Charger Behavior¶
In the default example the charger has a rated voltage and power. This has been changed to rated voltage and current:
Level 1: 120V, 15A
Level 2: 240V, 30A
Level 3: 630V, 104A
def get_charger_ratings(EV_list):
"""
This function uses the pre-defined charging powers and maps them to
standard (more or less) charging voltages. This allows the charger
to apply an appropriately modeled voltage to the EV based on the
charging power level
:param EV_list: Value of "1", "2", or "3" to indicate charging level
:return: charging_voltage: List of charging voltages corresponding
to the charging power.
"""
out = []
# Ignoring the difference between AC and DC voltages for this application
charge_voltages = [120, 240, 630]
charge_currents = [15, 30, 104]
for EV in EV_list:
if EV not in [1, 2, 3]:
out.append({"Vr": 0, "Ir": 0})
else:
out.append({"Vr": charge_voltages[EV - 1], "Ir": charge_currents[EV - 1]})
logger.debug(
"EV {} ratings: Vr = {} Ir = {}".format(EV, out[-1]["Vr"], out[-1]["Ir"])
)
return out
The charging function, \(V_{ch}(I_{b})\) is implemented voltage_update in Charger.py. It considers 4 different cases (the very first if statement is an initialization option):
Case 1: Current is within tolerance \(\epsilon\) of rated current \(\to\) voltage remains the same.
Case 2: Current is below rated current and voltage is below rated voltage \(\to\) voltage is increased via bisection search.
Case 3: Current is below rated and voltage is rated voltage \(\to\) retain rated voltage.
Case 4: Current is greater than rated current \(\to\) reduce voltage via bisection search.
def voltage_update(
charger_rating, charging_current, charging_voltage=None, epsilon=1e-2, quiet=False
):
if charging_voltage is None:
return {"V": charger_rating["Vr"], "Vmin": 0, "Vmax": charger_rating["Vr"]}
if abs(charging_current - charger_rating["Ir"]) < epsilon:
# Constant current charging: do nothing
pass
elif (charging_current < charger_rating["Ir"]) and (
charging_voltage["V"] < charger_rating["Vr"]
):
# increase voltage
charging_voltage = {
"V": (charging_voltage["Vmax"] + charging_voltage["V"]) / 2,
"Vmin": charging_voltage["V"],
"Vmax": charging_voltage["Vmax"],
}
elif (charging_current < charger_rating["Ir"]) and (
abs(charging_voltage["V"] - charger_rating["Vr"]) < epsilon
):
# constant voltage charging: do nothing
pass
elif charging_current > charger_rating["Ir"]:
# decrease voltage
charging_voltage = {
"V": (charging_voltage["V"] + charging_voltage["Vmin"]) / 2,
"Vmin": charging_voltage["Vmin"],
"Vmax": charging_voltage["V"],
}
else:
raise ValueError(
"voltage_update: inputs do not match any of the expected cases"
)
return charging_voltage
Battery Model Development¶
In order to achieve the desired charging profile, a fictitious battery resistance \(R(soc)\) is used. As this \(R\) increases the voltage must increase to maintain the rated current \(I_{\text{rated}}\) until \(V_{\text{rated}}\) is reached and held, at which point the current begins to taper.
We utilize the following design criteria:
The actual internal resistance of a battery is about on the order of 0.5 \(\Omega\)[1], which will be used as the \(R(soc=0)\)
We would like constant current charging until around \(soc=0.6\).
Charging is considered full when current drops below 3% rated.
From Criteria 2 we have \(R(0.6) = V_{\text{rated}}/I_{\text{rated}}\). For the three charger types we have defined that is:
Level 1: \(R(0.6) = 120\text{V}/15\text{A} = 8 \Omega \)
Level 2: \(R(0.6) = 240\text{V}/30\text{A} = 8 \Omega \)
Level 3: \(R(0.6) = 630\text{V}/104\text{A} \approx 6 \Omega \)
Splitting the difference we fix \(R(0.6) \overset{!}{=} 7\Omega\).
From Criteria 3 we have \(R(1) = V_{\text{rated}}/(0.03\cdot I_{\text{rated}})\). For the three charger types defined that is:
Level 1: \(R(0.6) = 120\text{V}/(0.03\cdot 15\text{A} )\approx 267 \Omega \)
Level 2: \(R(0.6) = 240\text{V}/(0.03\cdot 30\text{A} )\approx 267 \Omega \)
Level 3: \(R(0.6) = 630\text{V}/(0.03\cdot 104\text{A}) \approx 202 \Omega \)
Taking the maximum (so we make sure the current decays at least to 3% rated by full charge) we fix \(R(1) \overset{!}{=} 267\Omega\).
the function \(R(soc)\) is now created as a two linear segments: one from 0 to 0.6 and the other from 0.6 to 1:
def effective_R(soc):
if soc >= 0.6:
return 650 * soc - 383
else:
return 10.83 * soc + 0.5

The current is then simply:
def current_update(charging_voltage, soc):
# Calculate charging current and update SOC
R = effective_R(soc)
# If battery is full assume its stops charging on its own
# and the charging current goes to zero.
if soc >= 1:
return 0
else:
return max(0, charging_voltage / R)
Iteration components¶
The majority of the iteration related code is found in iterutils.py in order to reuse it in both Battery.py and Charger.py.
Before diving into the details, HELICS has iteration requests and results. The requests are passed as inputs and the results are returned (see the User Guide section on iteration for further details).
The relevant requests are:
NO_ITERATION: this forces movement to the next time step and should therefore be avoided by all Federates if iteration is desired.FORCE_ITERATION: this forces iteration. If a federate always requests this the simulation will be stuck in a never ending loop. It is intended to be used only in rare cases.ITERATE_IF_NEEDED: in this case iteration only takes place if new values are published. This is the usual flag that should be used when iteration is desired.
The last point is critical; HELICS uses the relevant outputs of other federates to determine if a given federate needs to iterate.
The relevant results are:
NEXT_STEP: simulation is moving on.ITERATING: simulation is still iterating.
Each federate should therefore look for NEXT_STEP in order to advance in time and otherwise continue to iterate at the current time.
Note: An essentially equivalent method to checking the flag for ITERATING or NEXT_STEP is to check whether the currently granted time is the same the previous one.
ITERATING \(\Rightarrow\) grantedtime == grantedtime_previous.
NEXT_STEP \(\Rightarrow\) grantedtime > grantedtime_previous.
Initialization¶
The first step is to initialize the federates.
In this step helicsFederateEnterInitializingMode is called and the federates publish their initial values.
The function is set_pub (with option init=True and logging commands taken out for clarity):
def set_pub(self, fed, pubid, pubvals, nametyp=None, init=False):
if init:
self.logger.info("=== Entering HELICS Initialization mode")
h.helicsFederateEnterInitializingMode(fed)
pub_count = h.helicsFederateGetPublicationCount(fed)
for j in range(0, pub_count):
h.helicsPublicationPublishDouble(pubid[j], pubvals[j])
The function call looks like:
# Battery.py
feditr.set_pub(fed, pubid, charging_current, "Battery", init=True)
# Charger.py
feditr.set_pub(fed, pubid, [x["V"] for x in charging_voltage], "EV", init=True)
Next, the federates iterate using helicsFederateEnterExecutingModeIterative.
The basic structure is:
Call
helicsFederateEnterExecutingModeIterative.If the result is
NEXT_STEPthen we’re done.
itr = 0 itr_flag = h.helics_iteration_request_iterate_if_needed while True: itr_status = h.helicsFederateEnterExecutingModeIterative(fed, itr_flag) if itr_status == h.helics_iteration_result_next_step: break
Get subscriptions. Done via the
get_subfunction:def get_sub(self, fed, subid, itr, valarray, valinit, nametyp, proptyp): sub_count = h.helicsFederateGetInputCount(fed) for j in range(0, sub_count): x = h.helicsInputGetDouble((subid[j])) if itr == 0: valarray[j] = [valinit] * 2 else: valarray[j].insert(0, valarray[j].pop()) valarray[j][0] = x
Here
valarraystores the current and previous value to check for convergence. The function call looks like:# Battery.py feditr.get_sub(fed, subid, itr, charging_voltage, vinit, "Battery", "voltage") # Charger.py feditr.get_sub(fed, subid, itr, charging_current, iinit, "EV", "current")
check error
If the error is sufficiently small loop back and do not publish, otherwise proceed to update and publishing, which will trigger another iteration. The function to check the error is
check_error:
def check_error(self, dState): return sum([abs(vals[0] - vals[1]) for vals in dState.values()])
The function call looks like[2]:
error = feditr.check_error(charging_voltage) if (error < epsilon) and (itr > 0): # no further iteration necessary continue else: pass
perform state update based on subscription values.
# Battery.py charging_current[j] = current_update(charging_voltage[j][0], current_soc[j]) # Charger.py charging_voltage[j] = voltage_update( charger_ratings[j], charging_current[j][0], charging_voltage[j] )
publish new outputs and increment iteration
# Battery.py feditr.set_pub(fed, pubid, charging_current) itr += 1 # Charger.py feditr.set_pub(fed, pubid, [x["V"] for x in charging_voltage]) itr += 1
Time Loop¶
The time loop looks almost identical to the initialization loop, except that instead of calling helicsFederateEnterExecutingModeIterative,
the call is to helicsFederateRequestTimeIterative:
itr = 0
itr_flag = h.helics_iteration_request_iterate_if_needed
while True:
grantedtime, itr_state = h.helicsFederateRequestTimeIterative(
fed, requested_time, itr_flag
)
if itr_state == h.helics_iteration_result_next_step:
break # Iteration complete!
else:
pass # Iterating
Similar to the initialization, it is critical to publish before the first time request, otherwise, HELICS will see no new data, and return NEXT_STEP.
The general simulation code is therefore:
while grantedtime < total_interval:
# Publication needed so we can actually iterate
feditr.set_pub(fed, pubid, publication_values)
# Time request for the next physical interval to be simulated
requested_time = grantedtime + update_interval
[...]
Note that this essentially means, that we publish our final values from time \(t\) as the very first thing in time \(t+\Delta t\).
Execution Results¶
Initialization Results¶
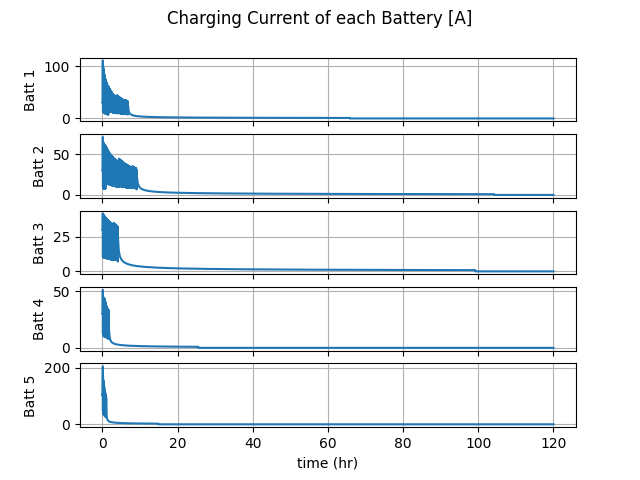
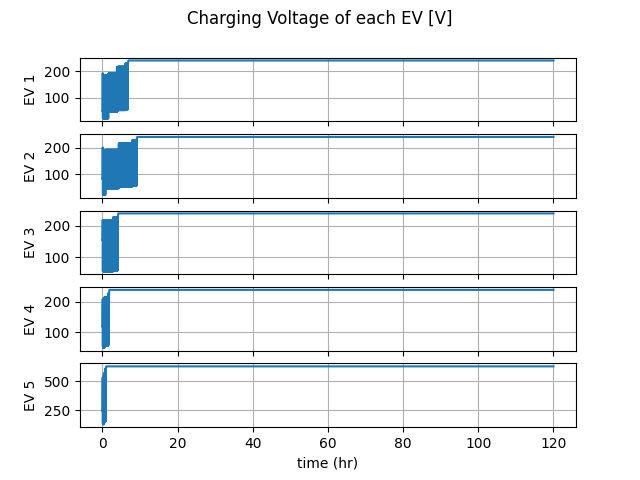
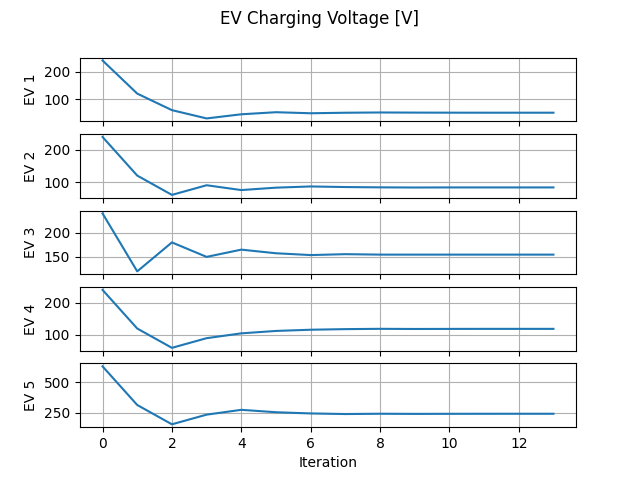
Two figures are produced following the initialization iteration, which show how the currents and voltages converge. Note that all batteries are in the constant current phase of charging, as such they all converge to their rated current (30A for EV1-EV4 and 104A for EV5). The voltages meanwhile are not nominal (240V or 630V) but rather determined based on the effective impedance, which is dependent on the initialized soc.

Time Loop Results¶
Four figures are produced once the co-simulation runs its course, two from Batter.py and two from Charger.py.
Battery Results¶
The Battery results show the the charging current in each battery, and the development of the SoC over time. As desired, the charging current exhibits the constant current followed by a decay characteristic, and the SoC rise to 1.


Charger Results¶
The Charger results show the how the voltage rises to its rated value and then remains there. The total power plot is also quite interesting Since initially the current remains fixed while the voltage rises, the total power draw increases. Once the charging mode switches to constant voltage and the current decreases the power draw follows suite.


Impact of Iteration¶
It is useful to think about why iteration would be necessary in a simulation in the first place. In a world governed by differential equations, iteration essentially smooths out timescales below the range of interest. It allows us to assume that quicker dynamics have already settled to their steady state. Power systems engineers might be quite familiar with this concept. The power flow, which assumes steady state of voltage and current dependencies, requires iteration because of the use of constant power loads. Dynamic simulations (in their simplest form), however, do not iterate, because all loads are converted to impedances. More advanced dynamic simulations do iterate because they are attempting to account for the impact of electromagnetic phenomena (e.g. power electronics control loops) that have already settled.
In this example, the charger needs to find the appropriate voltage to achieve rated current. In reality, there are a multitude of possible control algorithms that might be implemented. The use of iteration here is an acknowledgement that this fixed point will be found, but at a timescale that is effectively “instantaneous” w.r.t. the interval of one hour used in the simulation. That is \(\Delta t_{\text{control}} \ll \Delta t\).
To illustrate this, a second copy of the iteration is available in the repository (Battery_noitermain.py, Charger_noitermain.py, and advanced_iteration_runner_noitermain.json) with the iteration turn off (except for initialization) using the flag iterative_mode = False.
A comparison of the two runs is presented below:
With Iteration |
Without Iteration |
|---|---|
|
|
|
|
|
|
|
|
Without iteration the “voltage hunting” that happens during the constant-current charging phase takes place over hours instead of instantaneously as is the case with iteration. During the constant voltage phase the two runs are identical, since there is no longer an interdependence between the federates.
Finally, it is worth noting that the oscillation observed here is a function of the convergence algorithm implemented (see function voltage_update).
A more sophisticated algorithm may lead to less oscillation.
For example, if the charger had a model of the battery SOC and its dependence on the equivalent resistance, it could estimate the current and thus obtain the right voltage immediately.
The point is, that the specific charger control architecture is not of interest in this simulation and iteration allows to abstract out the implementation without completely neglecting certain model interdependencies and focus on behavior in the time frame of interest.
Questions and Help¶
Do you have questions about HELICS or need help?
Come to office hours!
Post on the gitter!
Place your question on the github forum!